Strelnitski teams with Olympic champion and longtime world record holder Yuri Sedykh to recommend more active use of hands and arms for advanced throwers.
By Vladimir Strelnitski, Springfield College, and Yuri Sedykh, Pole Universitaire Leonard de Vinci, Paris, France
Abstract
Contrary to widespread opinion, in advanced hammer throwing technique the arms are not a passive continuation of the hammer’s wire but rather an active driver of the hammer. Braced to form a rigid “triangle,” preventing sideways movements relative to the torso, the arms increase the radius of the “drive circle,” which increases the tangential force accelerating the hammer along its orbit.
Introduction
Although any throwing implement—discus, shot, javelin, or hammer—is sent to flight by the hands of the thrower, the laws of physics tell us that the primary source of energy and momentum imparted to the implement to secure its maximal possible release velocity are the legs of the thrower interacting with the ground. One of the first problems every hammer coach encounters while working with beginners is to prevent throwers from the natural desire to use their arms and hands primarily to move the hammer.
“Don’t bend the elbows, relax your arms completely!”—doesn’t this coach’s command sound familiar? The ultimate goal of the coach, in many cases, seems to be making the arms a completely relaxed continuation of the hammer wire. This is certainly preferable to strained arms with bent elbows. However, does it mean that, in contrast to the shot or javelin, the arms should play no role in the hammer throw? Here, based on the rich personal experience of one of us (Professor Sedykh), and on theoretical considerations, we present some arguments in favor of an active participation of the arms in the process of hammer acceleration.
The arms-chest “triangle”
Historical videos of hammer throwing available online, from the beginning of the 20th century till the present, show that before the 1960s it was customary to “drag” the hammer in turns, pull it with the left arm and shoulder stronger than with the right arm and shoulder and lead the movement with the head turned to the left, as if the thrower wants to see in advance where he or she drags the hammer. Starting in the late 1960s, more and more throwers were abandoning this technique.
Probably the first who did that was the Soviet thrower Romuald Klim, the 1964 Olympic champion, who also established a world record in 1969—74.52 (244-6). In the new technique, the thrower is supposed to look in the direction of the hammer and keep a rigid isosceles triangle made by the arms and the chest, from the entry into the first turn to the release. Most contemporary elite throwers follow this pattern. The better the thrower, the more symmetric, “more isosceles,” the arms-chest triangle is. An example can be seen at https://www.youtube.com/watch?v=mTlReluteEQ .
“Keeping the triangle” means that the muscles responsible for the sideways movements of the arms relative to the torso are braced. However, the arms must have the freedom to move up and down following the orbit of the hammer. Contrary to common belief, the hammer and the thrower’s body do not rotate around the same axis. The axis of the hammer rotation is inclined by 15-30° from the vertical in the direction opposite to the direction of the throw in the first turn and by ~40° in the last turn, whereas the axis of rotation of the thrower’s center of mass is also inclined back but much less than the former axis. This difference in the axes’ inclination causes a “flapping” motion of the arms relative to the torso during the turns. Thus the shoulder line should work like a cylindrical pivot allowing the rotation of the arm triangle in a vertical plane but preventing any sideways movements relative to the torso.
The “drive circle” and the acceleration of the hammer
The orbit of the hammer’s ball during its acceleration in turns can be described as a three-dimensional spiral—a sequence of inclined circles whose center propagates, from turn to turn, in the direction of the throw. The thrower accelerates the orbital speed of the ball in each turn by pulling on the wire in a special way: ahead of the momentary center of hammer rotation.
Slightly simplifying the situation, one can imagine the hammer as a “whip” with a heavy ball at the end of its “lash” (whose role is played by the wire and the arms), the other end being the midpoint between the thrower’s shoulders (Figure 1).

This latter point (we call it “Point X”) is where, effectively, the “lash” of the “whip” is attached to its “handle”– the torso of the thrower. The thrower accelerates the hammer by moving the torso so that Point X follows a “drive circle” whose radius ρ is smaller than the radius r of the hammer’s orbit.
The acceleration occurs because Point X is moved along the drive circle with a lead angle ϕ relative to the line connecting the ball of the hammer with the center of rotation (Figure 1). This makes the force of the pull Fp resolvable into two components: the centripetal force Fcp that keeps the ball on a circular orbit, resisting its tendency to move by inertia along a straight line, and the tangential force Ft that accelerates the hammer along its orbit.
It can be shown that the acceleration of the hammer is most efficient when the direction of the drive is perpendicular to the direction of the hammer motion. In this optimal case (it is shown in Figure 1), the tangential force speeding the ball up is
Ft = Fp • ρ / L ,
where L is the length of the “lash” (wire plus arms). Thus, the force accelerating the hammer is directly proportional to the radius of drive.
Driving the hammer with the hands?
The situation presented in Figure 1 corresponds to the throwing style in which the shoulders are completely relaxed, the arms are passive, and the midline of the arm “triangle” is a mere continuation of the hammer’s wire. This model is an adequate first approximation to the physics of the hammer acceleration, and a good theoretical guide for athletes of the initial and intermediate levels. However, with the development of technical skills, when the basic principles of the rotation with the hammer and, in particular, the correct footwork and the comfortable mechanical balance of the thrower/hammer system (sufficient countering of the hammer) have become more or less automatic, the thrower may wish to increase the efficiency of the hammer acceleration by using his/her arms and hands more actively.
Suppose the thrower keeps moving the Point X along the same drive circle as before, keeping the freedom of the up and down movements of the arm “triangle” (to account for the difference of the hammer and thrower axes of rotation), but braces the muscles that control the sideways movements of the “triangle.” The acquired stiffness of the connection between the torso and the arms excluding their relative sideways movements will allow the hands to be on the forefront of the hammer acceleration—to “push” the hammer actively to the left. This will break the straight-line wire/arms and will effectively move the Point X farther from the axis of rotation increasing the radius of drive from ρ1 to ρ2 and the drive angle from ϕ to ϕ + ∆ϕ (Figure 2). Now the role of the handle of the whip is not played by the torso alone, but by the torso plus arms, and Point X shifts from the shoulders area to the hands.
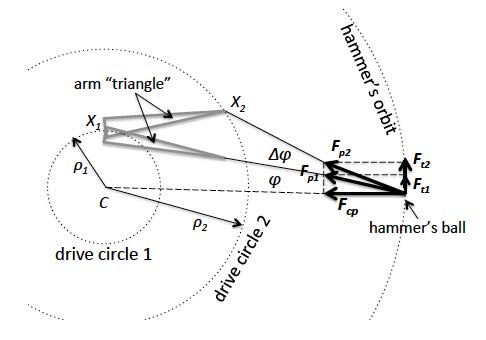
for better clarity on the figure.
The case marked in Figure 2 with the sub-index “1” corresponds to the original model, where the arms are just a continuation of the wire of the hammer. The base of the “arm triangle” moves counterclockwise along the circle of drive of radius ρ1. The pull of the hammer with the force Fp1 creates the centripetal force Fcp and the tangential force Ft1.
The case marked with the sub-index “2” corresponds to the modification of the “whip” model when the “handle of the whip” includes not only the torso of the thrower but also the arms firmly braced to the torso, so that the torso and the arms rotate as a unit. It is seen that the increase of the drive radius and the lead angle due to the inclusion of the arm triangle into the “handle of the whip” tends to increase the tangential component of the pull force (Ft2 > Ft1) and thus the effectiveness of the hammer acceleration.
Conclusion
We conclude that an advanced thrower should use not only his/her legs and torso in the double support phase, while accelerating the hammer between its highest and lowest points, but should also use the arms and hands actively pushing the hammer to the left and down. In the single support phase the thrower does not influence the hammer actively, and the arms can be completely relaxed, without breaking the symmetry of the “triangle.”